Graph Theory

A good way to learn about graph theory is the Konigsberg bridge problem. The town of Konigsberg had a river flowing through it, the river divided the city into four regions, which were connected by seven bridges. The question arose of whether it might be possible to take a walk through the city, crossing every bridge only once.

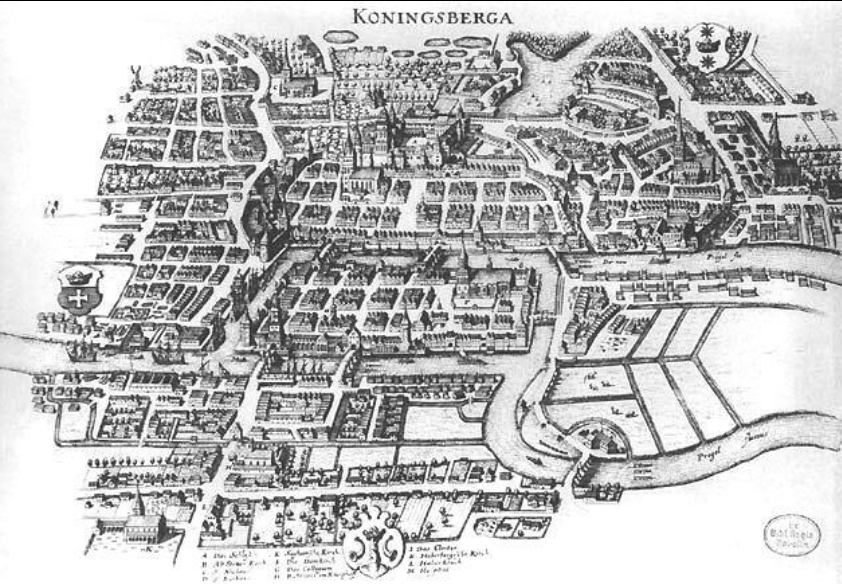
We can simplify the map by replacing each region with a vertex and each bridge with an edge between two vertexes:

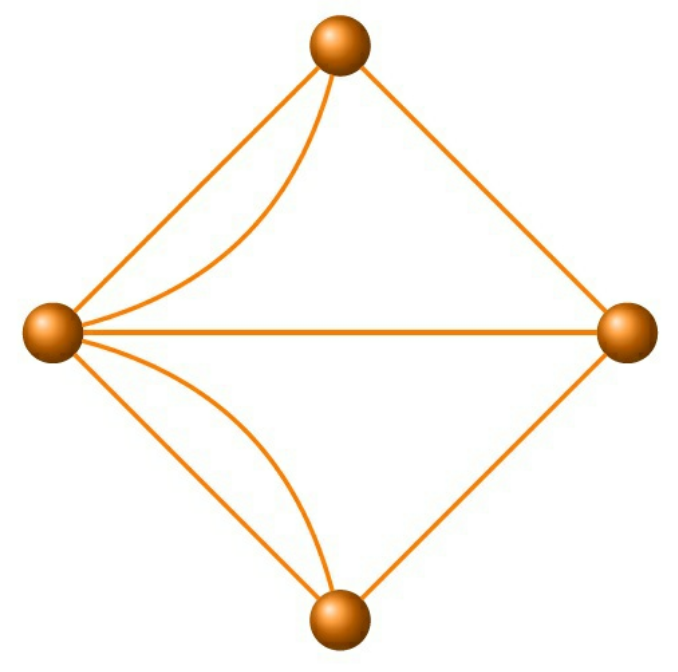
The key logical insight is to enter and leave a landmass requires two separate bridges, so any landmass which is not the starting or ending position must be the endpoint of an even number of bridges. In the case of Konigsberg, all four regions contained an odd number of bridges, making the problem unsolvable. A path through a graph which visits every edge exactly once is now called an Eulerian path.

Converting the map to a graph allows us to avoid Parkinson’s Law of Triviality.

A graph is a way of representing relationships in a set of data. When discussing the size of a graph, we often use ‘n’ for the number of vertices (nodes) and ‘m’ for the number of edges. The amount of space the graph requires depends on how we store the data. Two common methods are adjacency lists and adjacency matrices.

• adjacency Lists: When using an adjacency list, each node of the graph is stored with a list of nodes to which it is adjacent.
• adjacency matrix: